Сегодня разберём ещё одну геометрическую задачу. Она интересна тем, что в ней проходит связь геометрии с тригонометрией. При этом ее решение очень простое и легкое. Кстати, такой вид задачи вы можете встретить в заданиях ЕГЭ и ОГЭ.
ЗАДАЧА

Прежде чем приступить к решению задачи, мы:
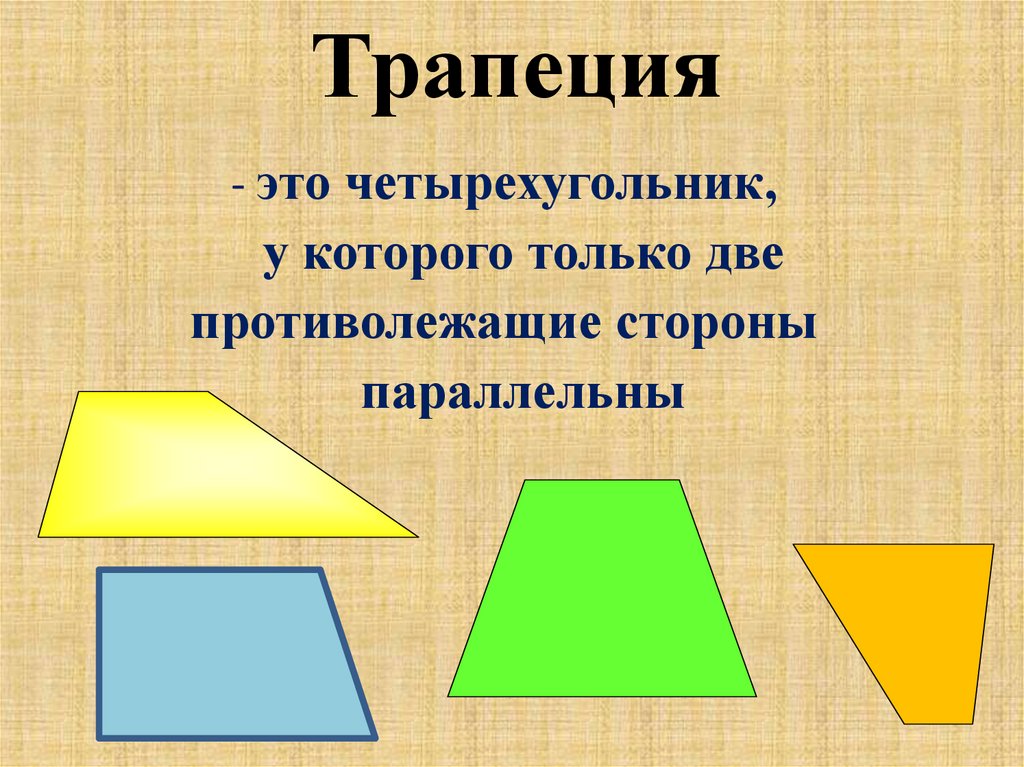
- — рассмотрим трапецию, вспомним ее основные характеристики;
- — перенесем данные задачи на чертеж;
- — внимательно прочитаем вопрос.
Как мы видим нам дана трапеция АВСD. Что мы знаем об этой фигуре? Давайте рассуждать:
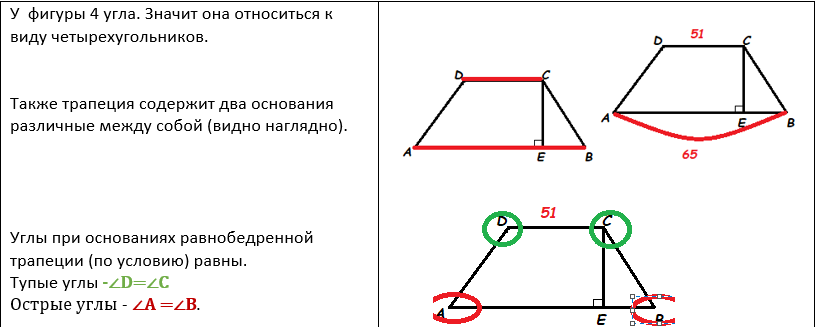
По условию задачи СЕ- высота трапеции.
Высота это- отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
ВИКИПЕДИЯ
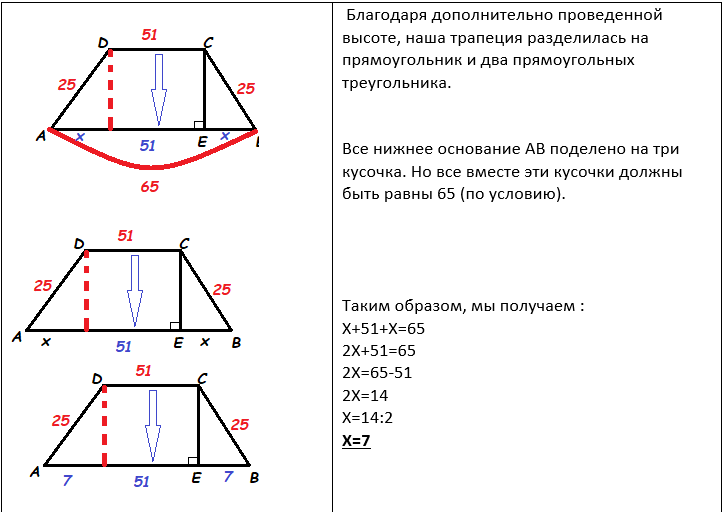
Проведем ещё одну высоту из точки D. Что нам это даст? Во- первых отметим ,что эти высоты равны друг другу. Во- вторых, построенная нами высота «отрезает» из нижнего основания кусочек равный 51. Наглядно это выглядит так:
Напомню, по условию, нам нужно найти синус острого угла трапеции. В нашей трапеции, как мы определили ранее, острые углы – А и В. Рассмотрим подробнее угол В в прямоугольном треугольнике СЕВ. Также вспомним, что синус острого угла – это отношение противоположного катета к гипотенузе прямоугольного ∆. Зная все это проведем следующие вычисления:
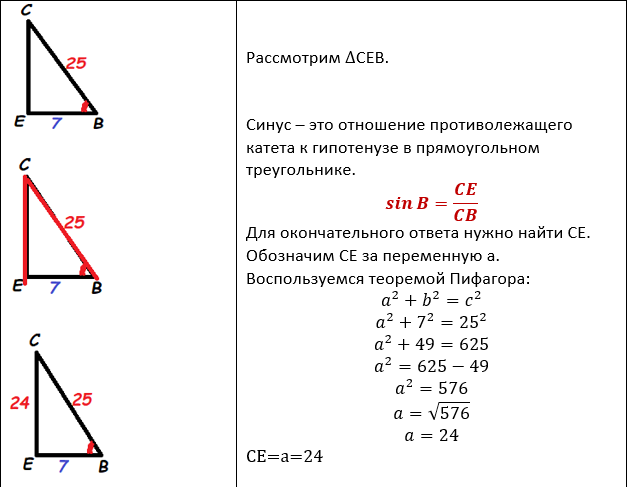
Вот мы и подошли к завершающему вычислению. Подставим наши данные и найдем ответ.

Как Вы сами убедились все достаточно просто и легко. Даже самые сложные задания можно разбить на ряд простых этапов. Мы с этим сталкивались в других заданиях как по алгебре, так и по геометрии. Удачи на экзаменах!!!!!