Сегодня мы разберем задачу по геометрии из ЕГЭ по профильной математики. Её мы можем встретить при решении третьего блока заданий. Сама задача не является сложной. Все решение состоит из ряда логических рассуждений, которые опираются на знание свойств того или иного элемента.
Однако, иногда при решении создается путаница. В свою очередь это ставит в тупик некоторых учеников и приводит их к неправильному ответу.
Хочется заметить, что для решения данной задачи можно использовать несколько способов. Мы же, разберем только один, но как можно подробнее.
ЗАДАЧА

Итак, приступим к рассуждению над данными этой задачи. Нам дана биссектриса АD ( по условию). Вспомним что это за элемент, какими свойствами он обладает.
Определение: Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла.
Шуточное определение: Биссектриса – это крыса, которая бегает по углам и делит угол пополам.
Мы видим, что данная биссектриса разделила основной треугольник АВС на два внутренних. Так же по условию АВ=АD=СD. Давайте отметим это условие на чертеже и подумаем, что нам это дает.

Наша биссектриса АD, выходя из угла А (∆ АВС) делит его на два одинаковых угла (св-во биссектрисы). Конечно, мы незнаем сколько градусов каждых из них. А то, что мы незнаем попробуем обозначить за Х (или любой другой переменной). Так как эти углы равны между собой наше рассуждение принимает следующий вид:

Что это нам дает? Продолжаем рассуждать…
Рассмотрим верхний треугольник АСD. Мы уже ранее определили его вид как равнобедренный. Для удобства развернем его. Перенесем все данные, которые уже есть на чертеже. Что мы видим?
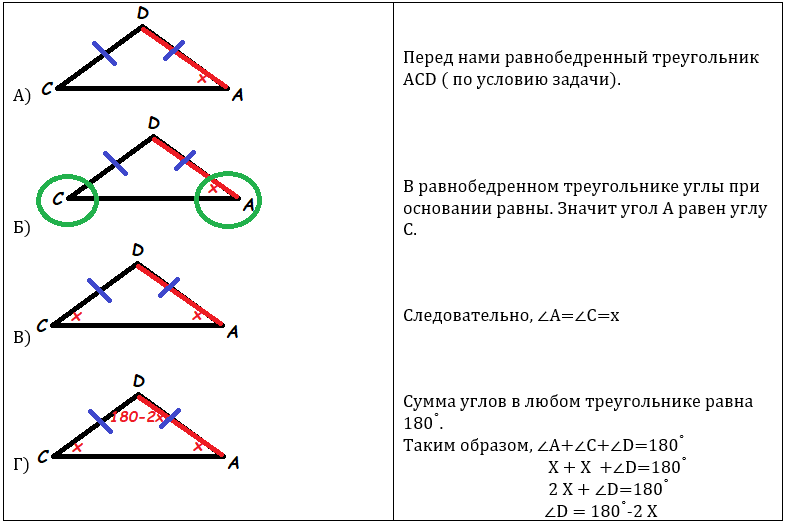
Внесем наши данные в основной чертеж. Получим следующее:
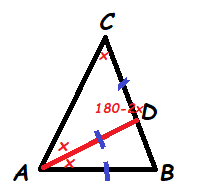
С верхним треугольником мы поработали, теперь нужно перейти в нижний. Как это сделать?
Обратим внимание на боковую сторону СВ основного треугольника, а также на биссектрису, проведенную к ней. Для удобства выделим эти элементы из основного чертежа и развернем их. Что мы увидим?

Наш основной чертеж пополнился данными (рис.1).
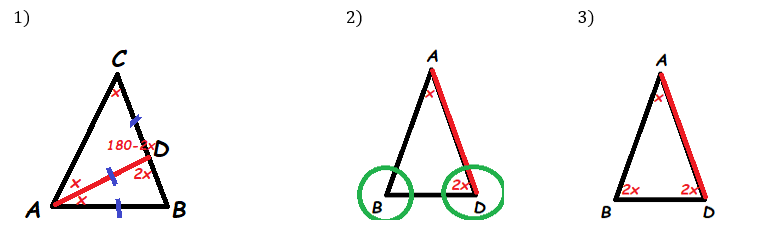
Благодаря нашим рассуждениям мы спустились в нижний треугольник АDВ. По условию задачи мы знаем, что он равнобедренный(рис.2). Следовательно углы при основании (∠D и ∠В) равны. Таким образом, как и в первом треугольнике, ∠D=∠В=2х (рис.3)
Наш итоговый чертеж, с учетом всех данных, выглядит так:
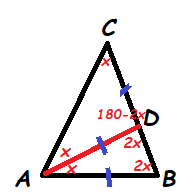
Вот мы и подошли к финальным вычислениям. Благодаря нашим логическим рассуждениям мы обозначили каждый угол основного треугольника. Что нам это дает? Все очень просто… Сумма углов треугольника равна 180˚. Собираем наши данные в уравнение:

Решить эту задачу можно и другими способами. Но если вы путаетесь в рассуждениях, не понимаете какие свойства задействованы, то данный материал будет полезен. Он наглядно раскроет вам все этапы решения.
Как я уже говорила, здесь больше рассуждений чем вычислительного процесса. Изучив этот материал и отработав его на практике, такие задачи будут решаться вами очень быстро.