Для начала, давайте рассмотрим основные типы задач, которые могут нам встретиться в третьем задании ЕГЭ по профильной математике. Их можно разделить на следующие группы:
Многоугольники: вычисление длин и углов.
Многоугольники: вычисление площади.
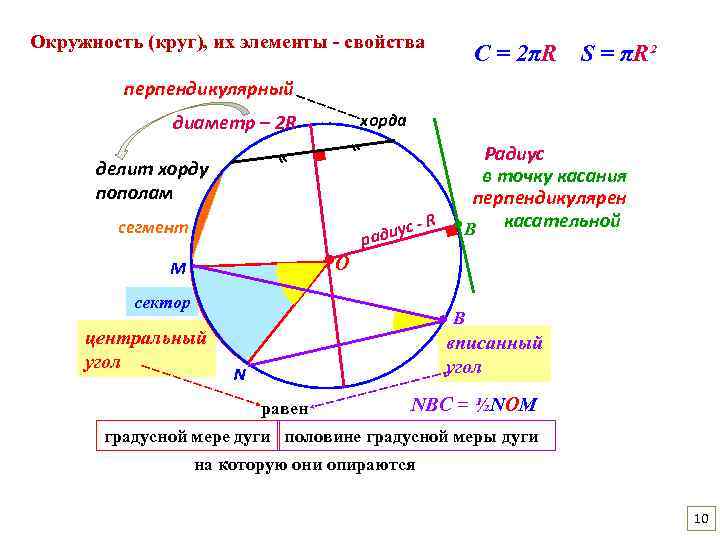
Круг и его элементы.
Координатная плоскость.
Как Вы увидели, группа многоугольники разбита на два типа.
К многоугольникам относятся такие фигуры как: квадрат, ромб, параллелограмм, и т.д. Произвольный многоугольник, с помощью дополнительного построения, может разбиваться на ряд других стандартных фигур. Этот метод чаще всего используется при нахождении площади произвольного многоугольника.
При решении третьего задания ЕГЭ по профильной математике, нужно показать знание основных формул, свойств геометрических фигур. Показать на практике навыки и умения применять их при решении задач.
Ряд заданий используют принцип работы в координатной плоскости или в квадратной решётки.
Давайте рассмотрим оба варианта:
Задание (первый тип)
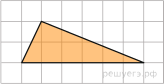
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Задание ( второй тип)
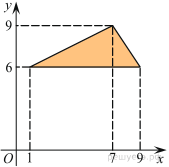
Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (7; 9).
Итак, в обоих заданиях нам нужно найти площадь фигуры. Отличие одной задачи от другой заключается в графическом виде представленной информации. В первой задачи работает принцип квадратной сетки, во второй принцип основанный на координатной плоскости. Как говорилось ранее, для решения такой задачи нужно:
1. Знать формулу нахождения площади представленной геометрической фигуры.
2. Найти, чему равна сторона, (или стороны), используя дополнительные построения.(В квадратной сетке по клеткам создаем прямоугольный треугольник так, чтобы искомая сторона стала гипотенузой, в координатной плоскости работаем по тому же принципу , но ориентируемся на значения цифр по прямым х,у)
3. По теореме Пифагора, находим чему равна сторона.
4. Подставляем в формулу площади и находим ответ.
Отдельно хочется рассмотреть задания, в которых дается произвольный многоугольник.
Задание
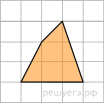
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Первый многоугольник, логично будет внутри разбить на ряд других геометрических фигур. Найдя сначала площадь каждой внутренней фигуры, а затем, сложив, полученные результаты, мы найдем ответ задания.
Задание
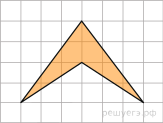
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Во втором случае, воспользуемся дополнительным построением и как-бы «обведем» наш многоугольник по границам, придавая ему стандартный вид квадрата (или прямоугольника).Для начала :
1. Найдем общую площадь внешней фигуры.
2. Найдем площадь каждой внутренней фигуры, не входящей в произвольный многоугольник.
3. Отнимем от значения общей площади все значения площадей ненужных внутренних фигур., тем самым найдем площадь оставшегося произвольного многоугольника. Это значение и будет нашим ответом.
Совсем другим типом задач являются задания на нахождение длин сторон, углов, дуг и т.д.
Здесь, прежде всего, проверяются знания свойств круга, внутренних и центральных углов, смежных и вертикальных углов, отношения вписанной описанной окружности.
Используются формулы теоремы Пифагора, тригонометрические значения sin, cos, формулы площади круга, нахождения радиуса и диаметра.
Обобщая, можно сказать, что при решении третьего задания ЕГЭ по профильной математике, мы говорим о проверке базовых знаний по геометрии, навыков и умения их применять на практике.