При решении уравнений, мы сначала определяем его вид. Так как, в зависимости от вида, выстраивается стратегия его решения. Сегодня мы поговорим о линейных уравнениях. А также, рассмотрим несколько примеров, которые относятся к данному типу уравнений. Таким образом, мы постараемся в этой статье разобрать следующие вопросы:
- Как решить линейное уравнение?
- Какие шаги входят в алгоритм решения?
- Как применить его на практике ?
Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная.
Стоит заметить, что данный вид является самым простым среди остальных видов уравнений. ( 9 задание ОГЭ_)
Для решения линейного уравнения достаточно придерживаться основного «базового» алгоритма. Давайте подробнее посмотрим каждый его шаг .
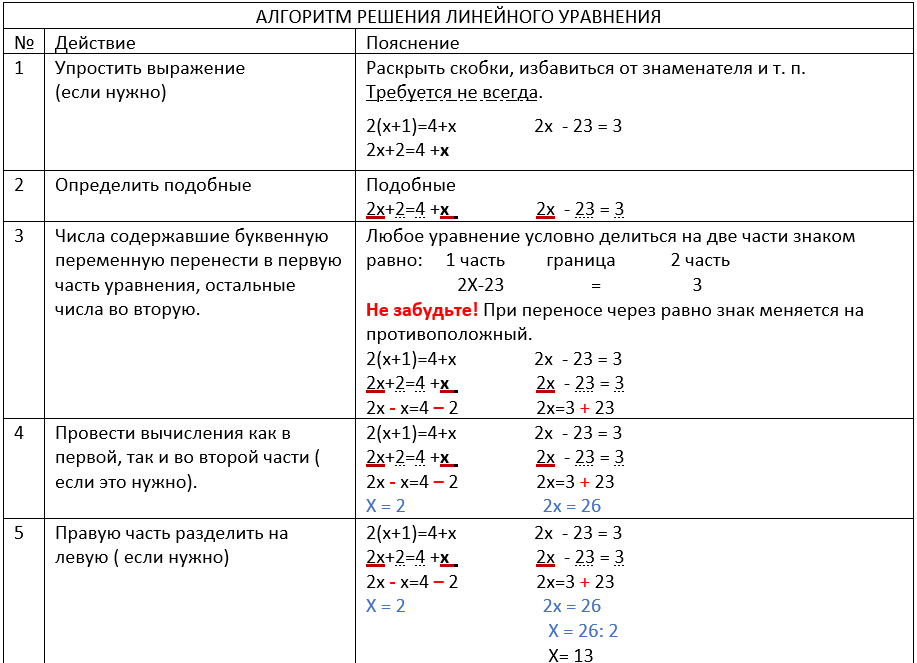

Применение алгоритма решения линейных уравнений на практике
Пример 1.
Найдите корень уравнения: х+4 = 2.
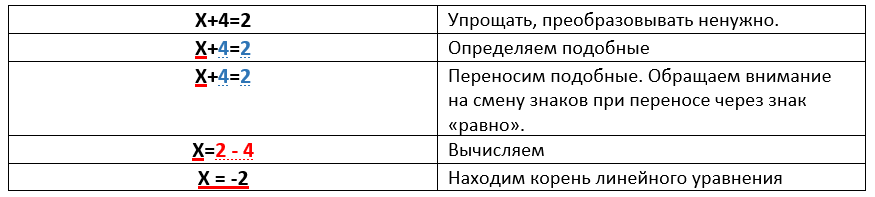
Пример 2.
Найдите корень уравнения 2(а-3)=4(а+1).
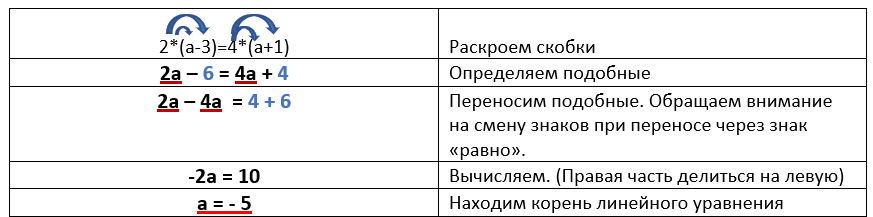
Пример 3.
Найдите корень уравнения.
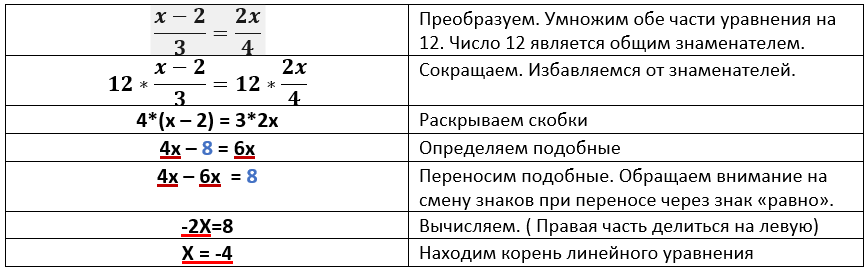
Итак, мы разобрали несколько типов линейных уравнений. Как видим, несмотря на небольшие нюансы, все уравнения придерживаются основного алгоритма решения.
Хочется напомнить, что, приступая к решению уравнений, придерживайтесь следующих правил:
- -Определите вид уравнения;
- — Вспомните алгоритм решения данного вида;
- — Не спешите, рассуждайте;
- — Следите за знаками чисел и переменных;
- — Не ошибитесь при итоговом вычислении.
Следуя этим простым правилам, поможет вам справиться с любым уравнением.







