В прошлых материалах, мы уже рассмотрели линейные, квадратные, логарифмические уравнения и т.д. Все эти виды мы можем встретить в 6 блоке заданий профильного ЕГЭ. Сегодня подробно разберем решение одного такого уравнения из этого блока. Данное уравнение относиться к тригонометрическому виду. Напоминаю, что все уравнения этого блока являются простейшими.
Прежде чем мы приступим, давайте вспомним таблицу тригонометрических значений:
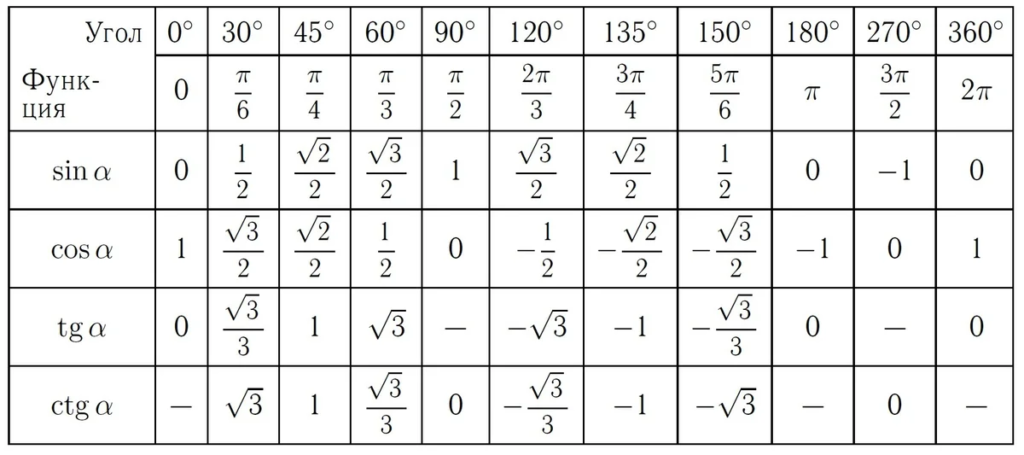
Ещё вспомним общий вид тригонометрических уравнений:
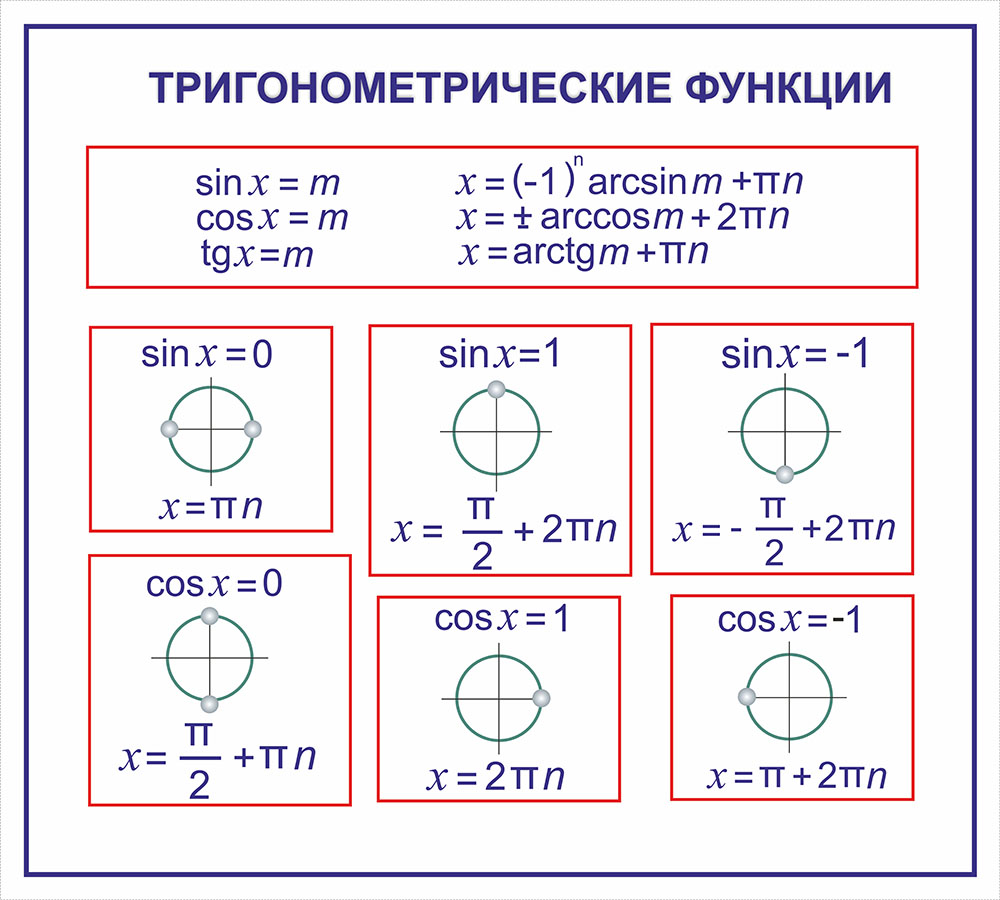
Приступим к разбору решений тригонометрического уравнения:
ПРИМЕР УРАВНЕНИЯ
Найдите корни уравнения:
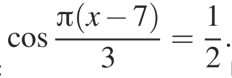
В ответ запишите наибольший отрицательный корень.

Для продолжения решения еще раз перечитаем условия уравнения. Нам требуется найти наибольший отрицательный корень. ( Чем меньше значение отрицательного числа, тем оно больше. -2>-12)

Как Вы видите решение достаточно простое. Главное знать значение тригонометрических функций и основные тригонометрические формулы. Подробное пояснение каждого этапа поможет вам при решении уравнений такого типа.