Все мы знаем общее определение квадратных уравнений. Сегодня же попробуем более «простым» языком поговорить об алгоритмах их решения. Почему алгоритмах? А потому что, квадратное уравнение может быть представлено в разных видах. Следовательно, каждый вид имеет свой алгоритм решения. Но не будем забегать вперед и начнем с самого начала.
Общий вид квадратного уравнения.
ах2+вх+с=0 где а,в,с, некоторые числа.
Почему данное уравнение называется квадратным? Потому что, максимальная степень переменной х в уравнении вторая. Кстати 2-ая степень также говорит о том, что максимальное число корней у данного уравнения тоже 2.
Например:
х5+2х3-х+7=0 — это уравнение пятой степени, а значит и максимальное количество корней не будет больше пяти. Может ли корней (ответов) быть меньше? Да, конечно. В некоторых же случаях уравнение вообще может не иметь решения.
Но вернемся к нашей теме. Квадратные уравнения бывают полного и неполного вида.
Рассмотрим таблицу:
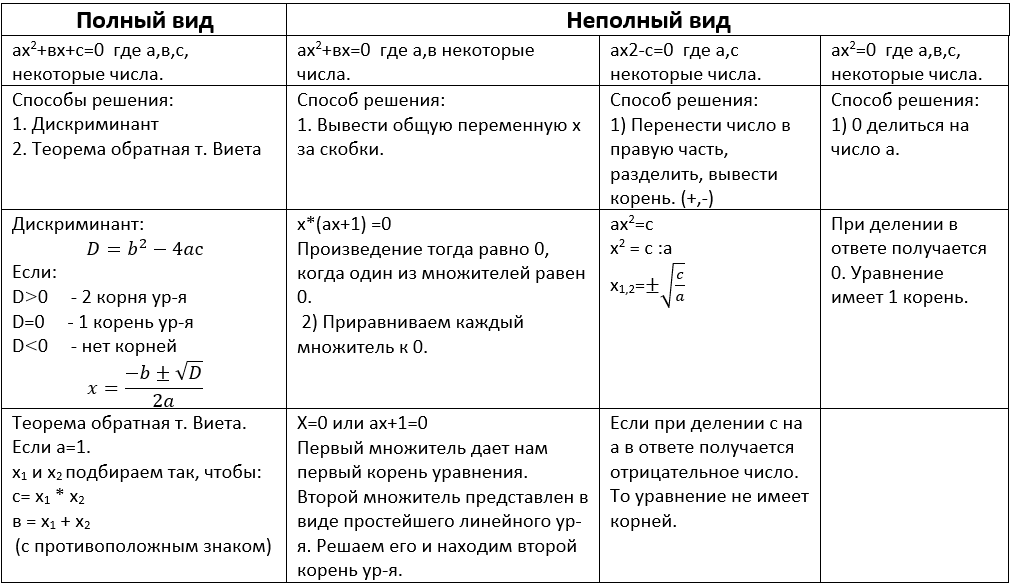
Применение алгоритмов решения на практике:
Найдите корни уравнения : х2-4х-12=0
а=1 в= -4 с= -12
Как мы видим, перед нами полный вид квадратного уравнения. Так как а=1, то данное уравнение можно решить двумя способами: по Дискриминанту; по теореме Виета.
Рассмотрим оба способа:

А теперь рассмотрим решение неполных квадратных уравнений:
6х2=-3х – перенесем – 3х в первую часть уравнения;
6х2 + 3х = 0 -неполный вид квадратного уравнения (а, в);
Х*(6х+3)=0 — вынесем х за скобку;
Х=0 или 6х+3=0 — произведение равно нулю тогда, когда один их множителей равен нулю;
Х1=0 или 6х= -3 — находим второй корень;
Х2= -0,5
Ответ: корни уравнения 0 и -0,5

Итак, мы разобрали основные этапы решения квадратных уравнений. Как мы убедились, алгоритмы решений различны. Мало определить тип уравнения, надо еще установить его вид (полное или неполное). От этого и будет зависеть алгоритм его решения. Пользуясь опорной таблицей, попробуйте самостоятельно выполнить несколько заданий.
И напоследок несколько советов:
Не спешите!
Придерживайтесь алгоритма решений!
Рассуждайте!
Больше практики!







