Вторым заданием в ЕГЭ по математике профильного уровня, является работа с графиком или диаграммой.
Основная задача в этих заданиях проверить навыки работы с графическими изображениями, получением данных и на их основании правильно определить ответ. Давайте рассмотрим два задания стандартного типа, в которых используются графики и диаграммы:
Задание с графиком.
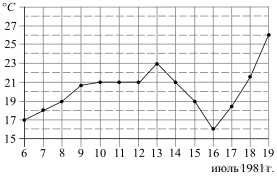
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.
Наибольшая температура 26 °, наименьшая 16°. Нам нужно определить разницу, т. е 26-16=10. Ответ 10.
Задание с диаграммой.
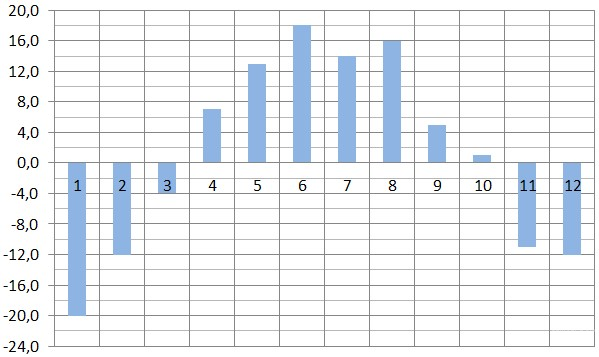
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году. Ответ дайте в градусах Цельсия.
Наибольшая температура 18 °, наименьшая -20°. Нам нужно определить разницу, т. е 18-(-20) =38. Ответ 38.
Как мы видим нам задания представлены в разных графических изображениях. Однако они имеют в своей основе один и тот же вопрос. Соответственно и алгоритм нахождения ответа идентичен.
Какие «подводные камни» мы можем встретить при работе с такими заданиями?
Во- первых, не всегда графики и диаграммы в ЕГЭ содержат все обозначения. Ученикам нужно самостоятельно, логически, доставить нужные обозначения для определения ответа. Например, внимательнее рассмотрим предыдущие задания, а точнее их графические изображения.
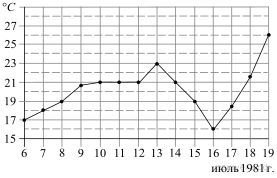
При нахождении наибольшей температуры по первому изображению, мы видим, что точка расположена на пунктирной средней линии между цифрами 25 и 27. Соответственно логично предположить, что пунктирная линия соответствует значению 26.
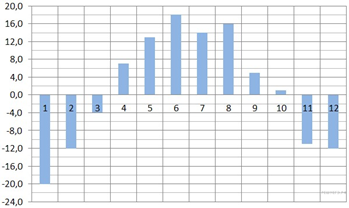
Рассматривая второе изображение (диаграмму), мы видим, что столбик наибольшей температуры соответствует средней линии между цифрами 16 и 20. Диапазон между ними равен 4 единицам. Средняя линия делит ее пополам. Таким образом, мы выяснили, что наибольшая температура равна 18, т.е. каждое деление увеличивается на две единицы.
Неправильно рассчитанные, в спешке, показатели могут привести к неправильному ответу.
Хочется отметить такие задания, в которых изображены измерения за весь год, а в вопросе спрашивают о значение наименышей (наибольшей) температуры за первое (второе) полугодие. То есть вам нужно работать только с определенными 6 месяцами, не беря во внимание показатели всего года.
Другой тип таких заданий может выглядеть так:
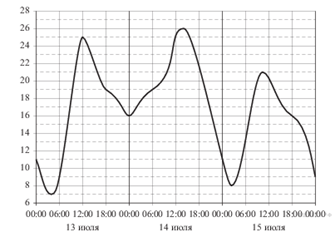
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 15 июля. Ответ дайте в градусах Цельсия.
Наибольшая температура 21 °, наименьшая 8°. Нам нужно определить разницу, т. е 21-8=13. Ответ 21
Обратите внимание, график содержит показатели за 3 дня. Вам же нужно найти разность температур только за 15 июля.
Иногда встречаются задания, которые содержат формулу. Сначала надо правильно по графику определить показатель, затем подставить его в формулу и после вычисления найти ответ.
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н · м? Ответ дайте в километрах в час.
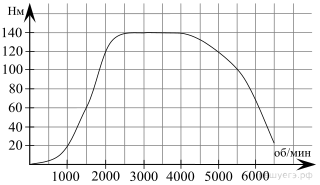
Для того, чтобы крутящий момент был не меньше 120 Н · м число оборотов двигателя в минуту n должно быть не меньше 2000 и не больше 5000 (см. график). Поэтому искомая наименьшая скорость определяется по формуле v = 0,036 · 2000 = 72 км/ч. Ответ 72.
Обобщая, можно сказать, что графики и диаграммы в ЕГЭ, представленные во втором задании, не сложные по своему содержанию и вычислению. При этом, нужно очень внимательно вчитываться в текст задания, осмысливать поставленный вопрос, изучить расстановку цифр. Спокойный и рассудительный подход поможет справиться с таким заданием с легкостью.