Документация, разработки уроков и другие материалы для учителя

Нестандартный, инновационный урок по геометрии позволит в форме сторителлинга (истории) познакомить учащихся с теоремой Пифагора. При объяснении (повествовании) учащихся ждет:

— знакомство с краткой исторической справкой о жизни и деятельности Пифагора;
— повторение основных терминов и их обозначения в геометрии;
-моделирование многоугольников из равносторонних прямоугольных треугольников;
— формулирование теоремы Пифагора и ее доказательство;
— практическое использование теоремы Пифагора в жизни.

На этапах урока:

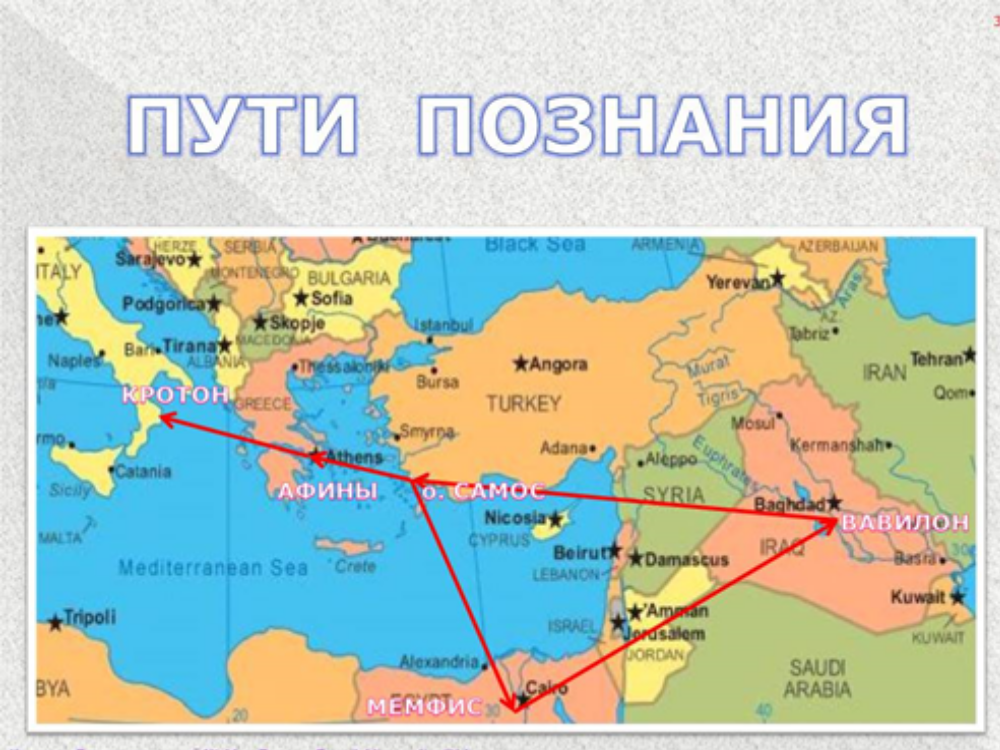
прослеживается межпредметная связь с математикой, историей, географией;
применяются методы и приемы ТРКМ и ТРИЗ;^{(ТРКМ-технологии развития критического мышления, ТРИЗ-теория решения изобретательских задач)}
исследуются разные направления применения теоремы Пифагора в реальных жизненных ситуациях.

Вид сторителлинга: повествование

Инфографика используется как дополнительный элемент истории.

Основная цель занятия:

— рассказать о великом ученом Пифагоре и его открытиях;
-ввести определение теоремы Пифагора;
-изучить доказательство теоремы и ее буквенное представление;
— показать разнообразие применения теоремы Пифагора в жизни человека.

Этапы занятия

1.Актуализация знаний.

— Этап введения в историю. Позволяет сконцентрировать внимание учащихся, задать нужную психологическую и эмоциональную атмосферу.

Геометрический диктант в форме интерактивной инфографики.(Приём “Диктант значений”)

Описание: приём экстраактивного обучения.. Преподаватель диктует не слова, а их значения. Ученики должны по значениям определить слова и написать их.

1.Как в геометрии называют предложение, непосредственно вытекающее из теоремы? (следствием).

2. Как называется утверждение, принимаемое без доказательства? (аксиома)

3. Часть плоскости вместе с ограничивающей ее замкнутой ломаной линией называется..(многоугольником).

4. Часть прямой, ограниченную точками с обеих сторон, называют ….(отрезком).

5. Прямая, имеющая с окружностью две общие точки, называется ….(секущей).

Учитель:

-Как интересно обратите внимание на первые буквы ваших ответов:

Следствие Аксиома Многоугольник Отрезок Секущая——-САМОС

Ученики: и что? Что это значит?

Учитель: дело в том, что так называется остров, где родился и жил великий ученный …

Ученики: Какой?

Учитель: хотите я расскажу Вам о нем? Мы познакомимся с его работами, узнаем, как мы используем его открытия в повседневной жизни?

Ученики: да!.

Учитель: тогда для начала расшифруйте его имя… Узнайте кто родился на острове Самос? (игровой момент)

2.Историческая справка

-Слышали о таком ученом? Знаете о его открытиях? (краткая биография)

3.Изучение нового материала.

Именно с именем Пифагора связанна следующая теорема:

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, например, древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным.

Прием: «Моделирование многоугольников»

Учитель:

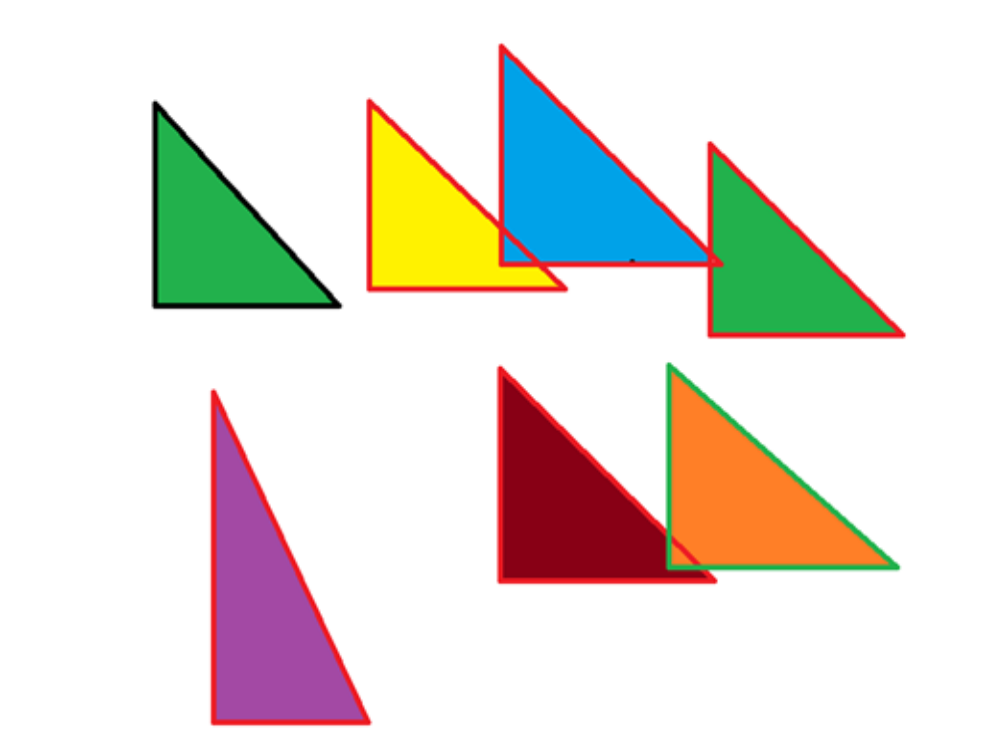
-Перед Вами несколько маленьких моделей треугольников. К какому виду они относятся? (равносторонние, прямоугольные)
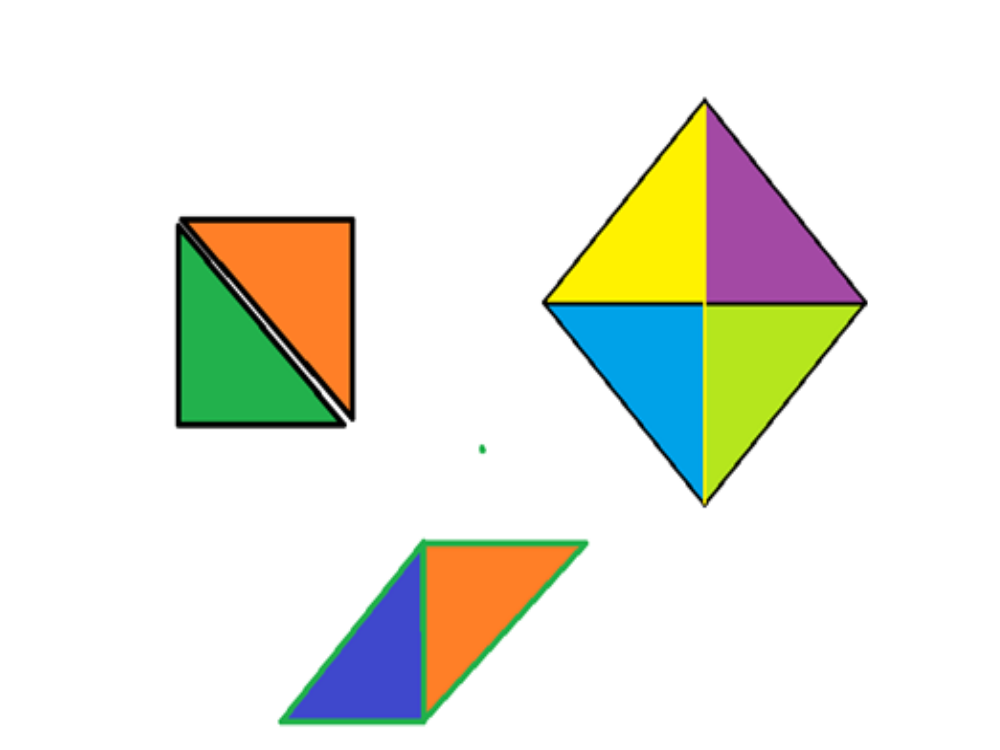
-Интересно, а какие ещё фигуры можно из них составить?

Практическое занятие на составление моделей квадрата, параллелограмма, ромба (составные многоугольники)

Учитель:

-Молодцы!

Возможно, Пифагор так же рассматривал, составлял модели и заметил закономерность, которую и сформулировал в теореме.

В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c²=a²+b².

Любую теорему надо доказывать и поверьте доказательств много, я же расскажу о одном веселом доказательстве.

4. Пифагоровы штаны на все стороны равны»

Это шуточная фраза, которая именует одно из доказательств теоремы Пифагора.

Рассмотрим наглядно рассмотрим данное доказательство с помощью приема «моделирования».

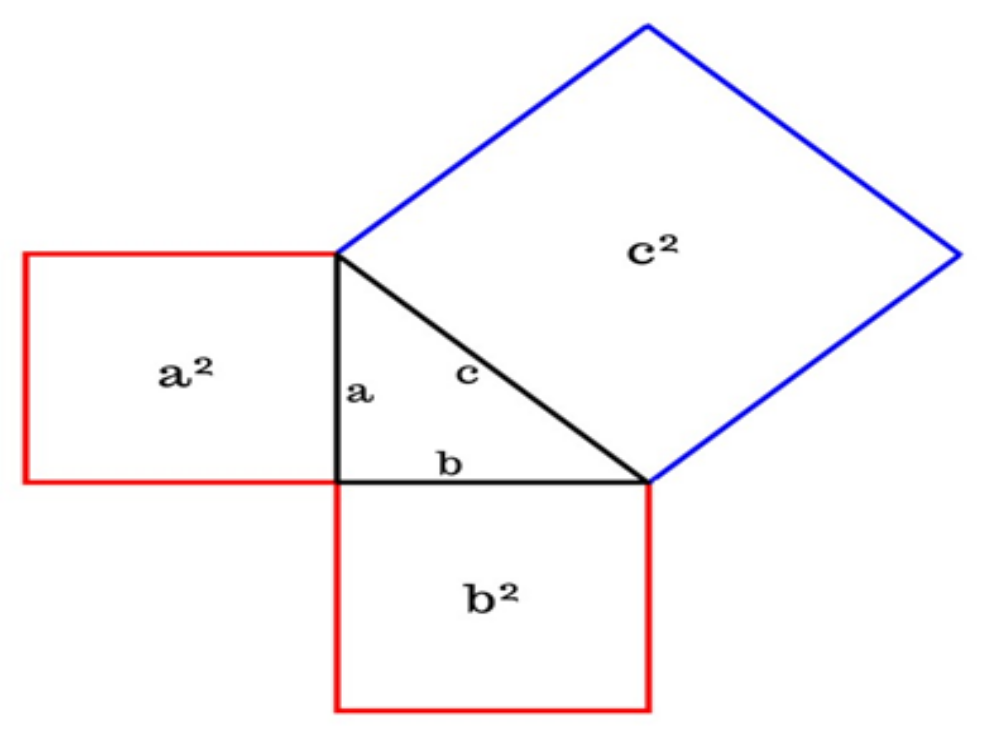
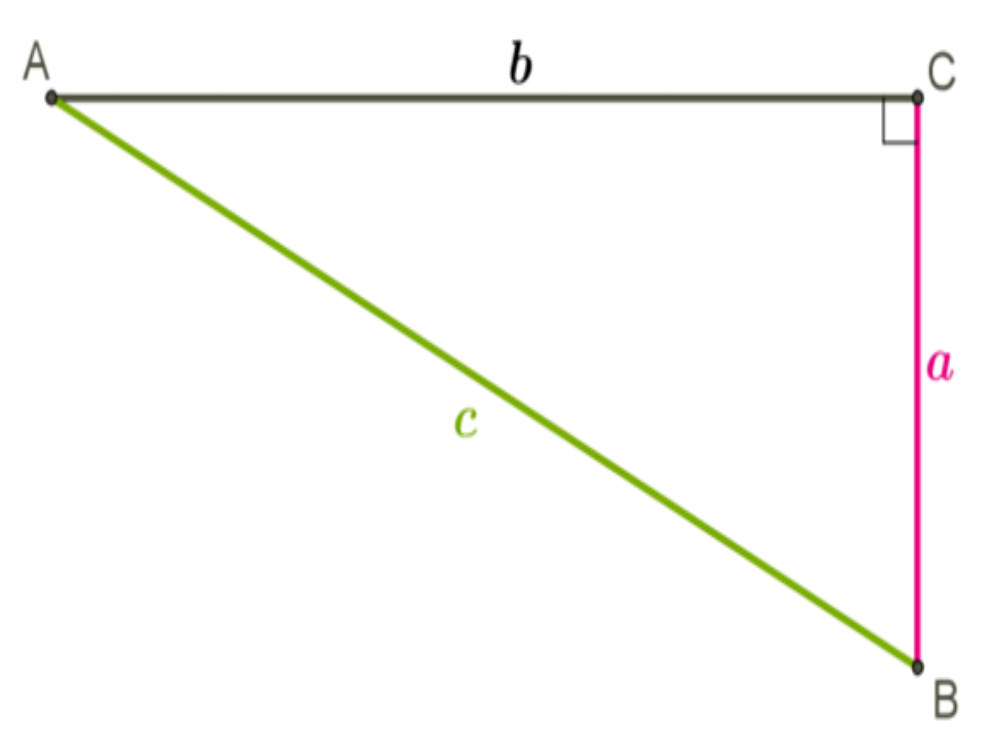
На этой фигуре c — гипотенуза, a и b — катеты.

Проведём перпендикулярную линию к гипотенузе (c):

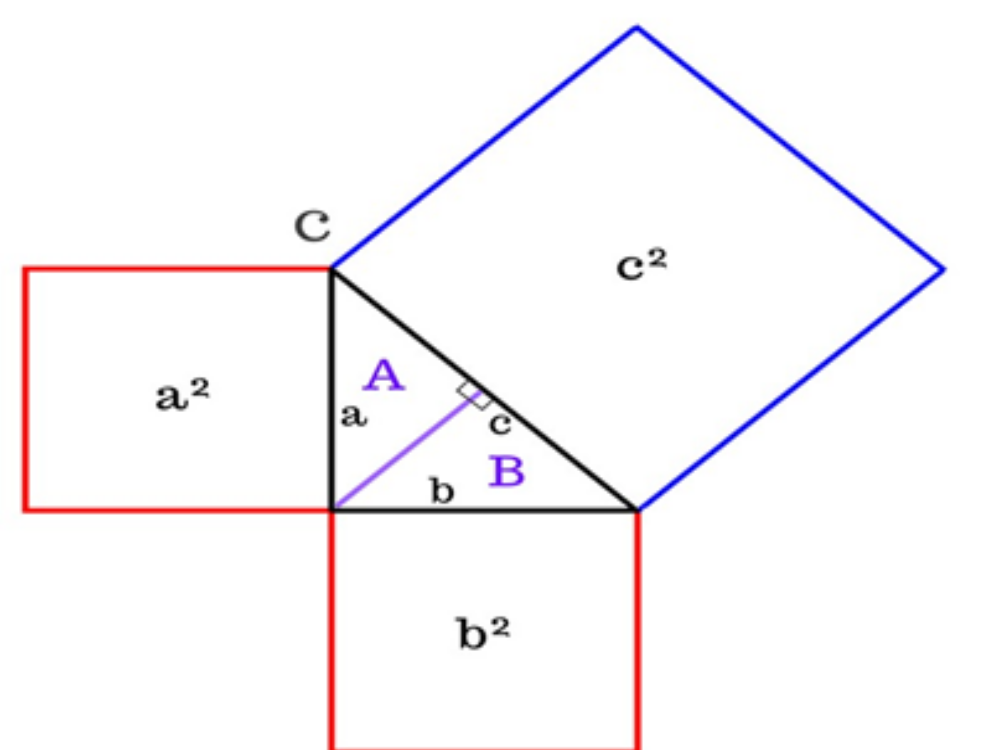
Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).

Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
Делим «Пифагоровы штаны» на 3 похожие фигуры:

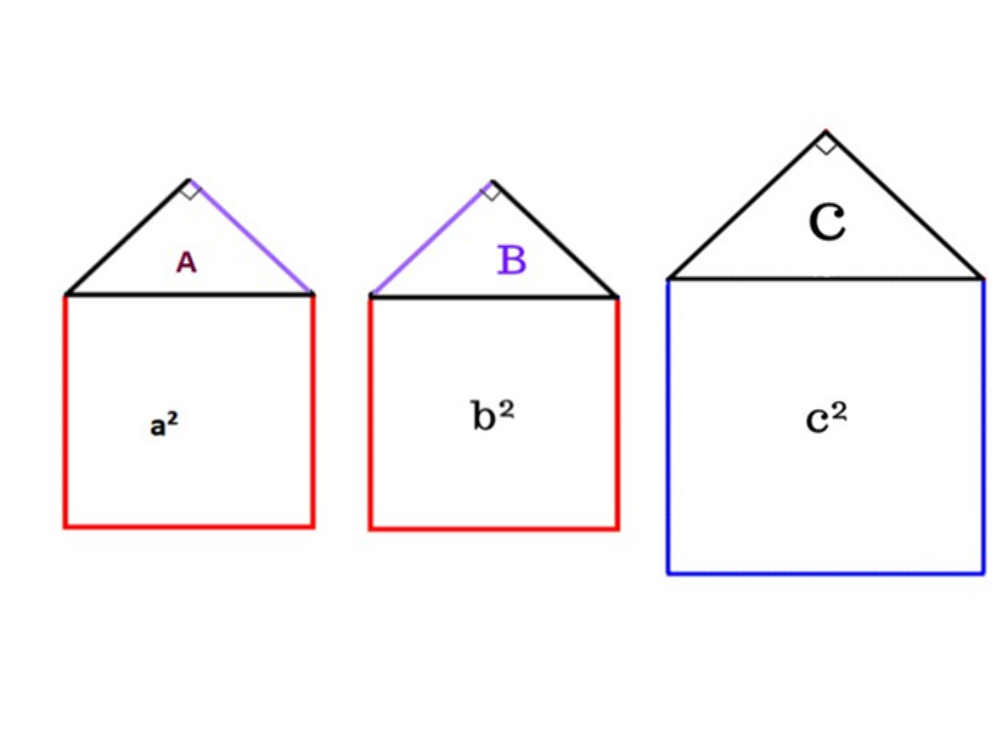
Все 3 треугольника подобны друг другу (A, B, C) и из-за этого «фигуры-домики» также являются подобными.
Значит соотношение площади A и a² будет одинаковым с площадью B и b², но и с площадью C и c². Т. е.: A/a² = B/b² = C/c² = β (назовём это соотношение греческой буквой бета);
Площадь каждого треугольника, через площадь каждого из квадратов, равна: A = βa², B = βb², C = βc²;
Вспомним, что С = А + B, т. е. βc² = βa² + βb², это равно c² = a² + b².

Что и требовалось доказать.

Рассмотрим наглядно еще один вид доказательства теоремы Пифагора;

5. Применение теоремы Пифагора в повседневной жизни..

Учитель: интересно, как и где может применяться теорема Пифагора? Как Вы думаете? Давайте подумаем, поразмышляем …..

Прием: «Мозговой штурм»

Учащиеся обсуждают направления, ситуации. Высказывают предположения. Задача учителя незримо направлять размышления в нужный контекст. Если ученики затрудняются с ответами продолжить повествование самостоятельно..

Примерные варианты:

В спорте…

Когда биатлонист стреляет по мишени, он делает «поправку на ветер». Если ветер дует справа, а спортсмен стреляет по прямой, то пуля уйдёт влево. Чтобы попасть в цель, надо сдвинуть прицел вправо на расстояние смещения пули. Для них составлены специальные таблицы (на основе следствий из т. Пифагора). Биатлонист знает, на какой угол смещать прицел при известной скорости ветра.

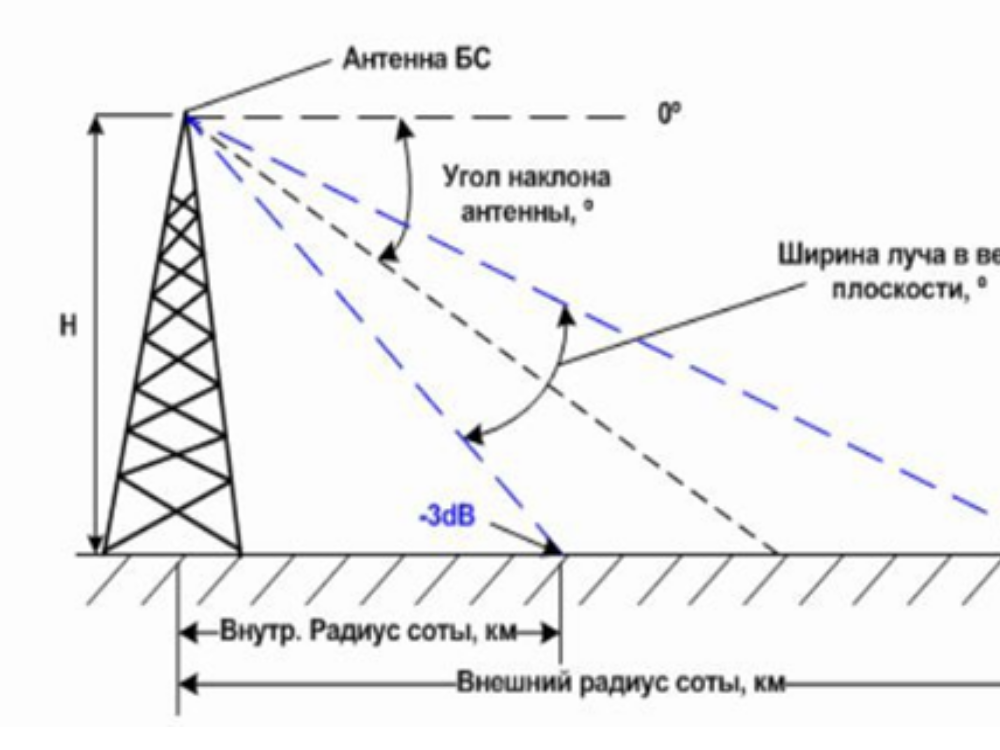
Сотовая телефонная связь..

Все понимают, что сейчас мобильный телефон очень важный атрибут жизни современного человека. Каждому абоненту важна качественная сотовая связь. А качество зависит от высоты антенны мобильного оператора. Чтобы рассчитать, в каком радиусе можно принимать передачу, задействуем теорему Пифагора.

При пожаре…

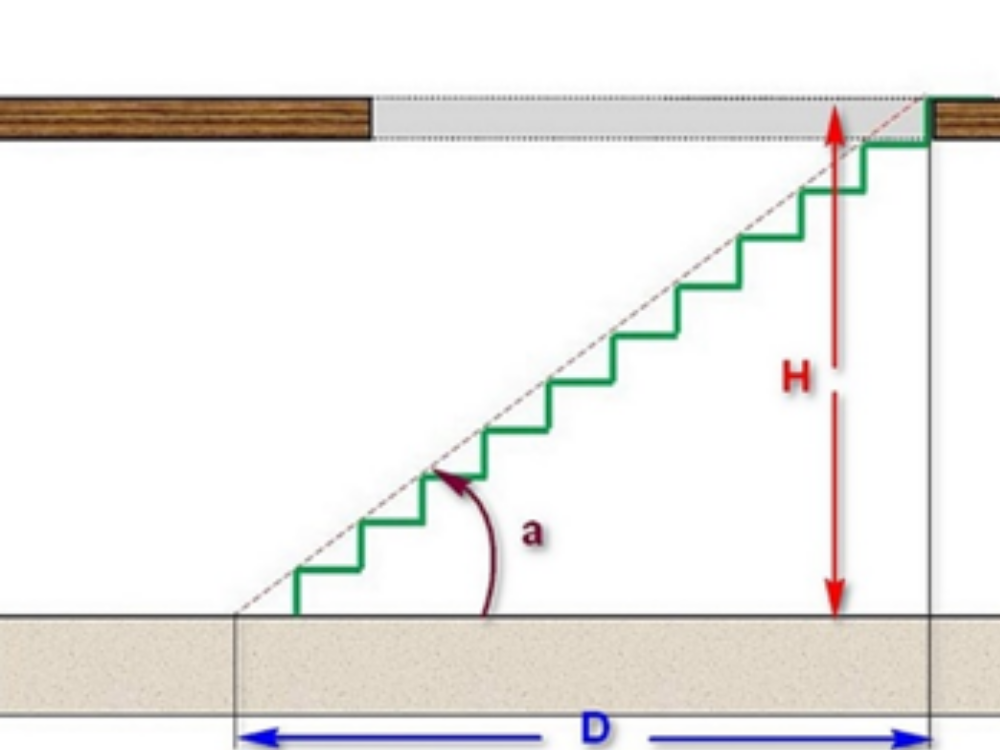
Как рассчитать длину лестницы при пожаре?

Нужно определить на каком расстоянии будет опираться лестница от возгорания и на какой высоте произошло возгорание. После, применяя теорему Пифагора, необходимо вычислить длину лестницы (гипотенуза).

В астрономии..

Явление звёздной аберрации, открытое в 1729 году, заключается в том, что все звёзды на небесной сфере описывают эллипсы. Большая полуось этих эллипсов наблюдается с Земли под углом, равным 20,5 градуса. Такой угол связан с движением Земли вокруг Солнца со скоростью 29,8 км в час. Чтобы с движущейся Земли наблюдать звезду, необходимо наклонить трубу телескопа вперёд по движению звезды, так как пока свет проходит длину телескопа, окуляр вместе с землёй перемещается вперёд. Сложение скоростей света и Земли производится векторно, используя т. Пифагора U²=C²+V²

При строительстве …

При строительстве постоянно необходимо решать вопрос о длине стропил для крыши, при условии, что уже изготовлены балки.

Пример: в доме по плану необходимо построить двускатную крышу. Какой длины должны быть стропила? Всё это представляется в виде треугольника и рассчитывается по теореме Пифагора.

Как мы убедились, основы теоремы Пифагора используются во многих направлениях нашей жизни.