Простые текстовые задачи встречаются в первом задании ( профильного уровня) экзамена по математике.
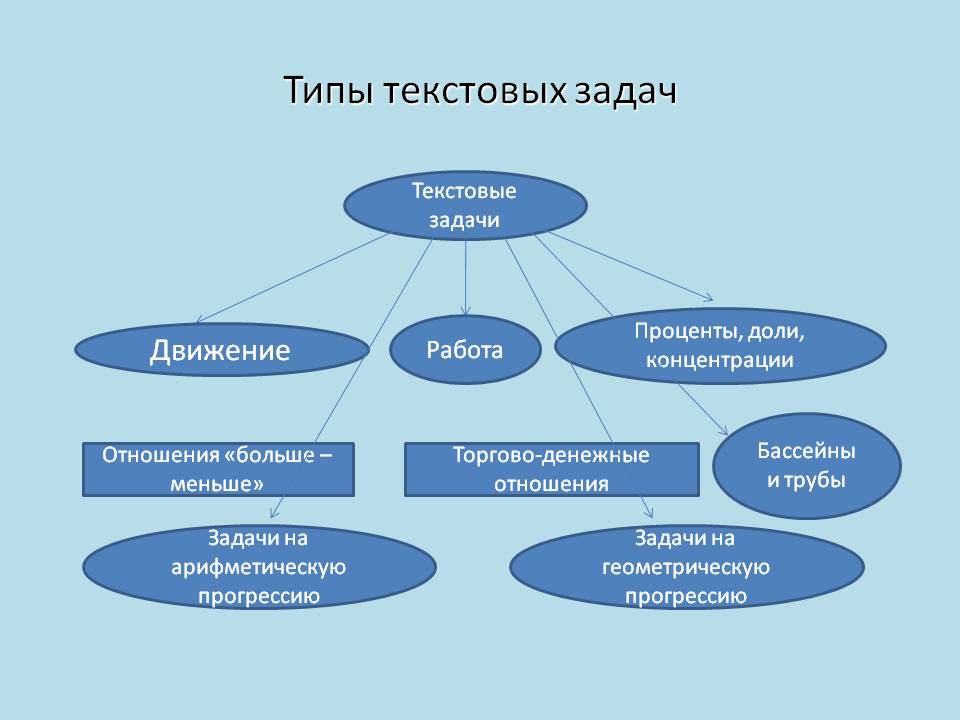
Виды таких задач делятся на :
- Вычисление
- Округление вниз
- Округление вверх
- Задачи на движение
- Задания содержащие разные величины
- Проценты
- Задачи содержащие логику.
В одной задачи может работать несколько видов. Например, задача на движение может содержать в себе различные величины и после соответствующего преобразования переходить к вычислительному процессу проходящего на основании формул движения.
Естественно вычисления проходят в любом виде задач, но правильно подойти к этому этапу помогут логика, составление пропорции и многое другое.
Давайте вспомним основные характеристики задач.

infourok.ru
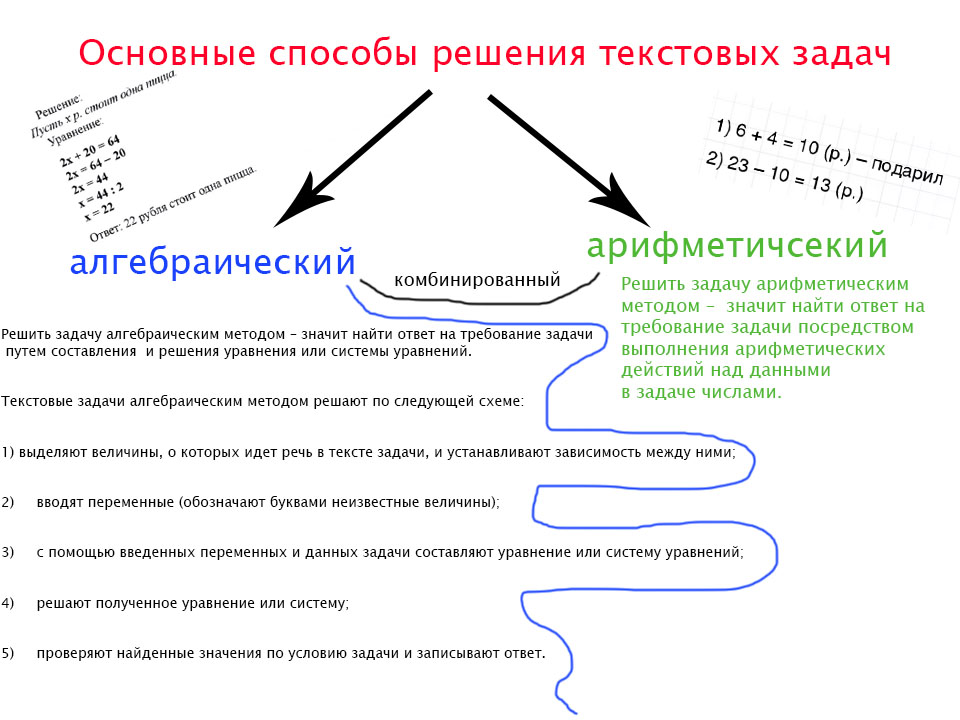
Давайте рассмотрим основные типы простых текстовых задач, выявим (если они есть) закономерности, распишем алгоритмы их решения и изучим несколько способов нахождения правильного ответа.
Простые текстовые задачи.
Задачи на проценты:
Шоколадка стоит 50 рублей. После проведенной рекламной акции цена на нее повысилась на 50 %. Сколько стоит шоколадка после повышения цены?
1 способ: 50 р-100% х= 50*50/100=25р.
Хр.- 50% 50 +25 =75 Ответ 75 рублей
2 способ: 100%+50%=150% 50р.-100% х=50*150/100= 75
Хр.- 150% Ответ 75 рублей.
Обратите внимание на такие слова как- скидка, наценка, уценённый товар, надбавка. Данные слова говорят о увеличении или уменьшении данных.
Задачи на логику и сообразительность с минимальным вычислительным процессом:
Саша живет в 5-ти этажном доме. В нем несколько подъездов. На каждом этаже 4 квартиры. В каком подъезде живет Саша, если номер ее квартиры 26?
5(этажей)*4(квартиры на этаже)=20 (квартир )-1 подъезд
Значит с 1квартиры по 20 будут располагаться в 1 подъезде, а номер квартиры Саши(26) будет во втором подъезде. Ответ:2
Иногда вопрос стоит не о подъезде, а о номере этажа на котором располагается нужная квартира.
Зная что на этаже по 4 квартиры, и нумерация квартир во втором подъезде начинается с квартиры №21, не трудно выяснить что квартира №26(Квартира Саши) располагается на 2 этаже.
Рассмотрим еще одну задачу. У Саши 26 рублей. Он хочет подарить цветы маме на день рождения. Мама очень любит розы. Одна роза в магазине стоит 6 рублей. Сколько роз он подарит маме?
Итак, сначала мы разделим 26 рублей( Саши) на 6 рублей (стоимость розы) и получим ответ 4 розы и 2 рубля останется. Саша может купить 4 розы, но вопрос стоял иначе-«Сколько роз он подарит маме?». Маме он подарит 3 розы.
Ответ данной задачи опирается но знания светского этикета ( принято дарить нечетное количество цветов). И хотя Саша имеет возможность купить 4 розы, подарит меме он только 3.
Или еще один вид простых текстовых задач:
Дейенерис Бурерожденная из дома Таргариенов, Королева Андалов и Первых Людей, Владычица Семи Королевств, Неопалимая, Разрушительница Оков и Матерь Драконов освобождает рабов города Миэрин. В первый день Дайенерис освободила половину всех рабов и еще одного. Во второй день – половину оставшихся рабов и еще одного и так далее. На десятый день ей осталось освободить всего лишь одного раба. Сколько всего рабов было в городе Миэрин?
Во всем условии этой задачи только в конце дают фактическое число, а это значит именно с конца будет проходить решение и нахождение ответа.
Начнем решать задачу с конца. Если в 10-ый день остался 1 раб, то в 9-ый день в городе было (1+1)⋅2=4 раба. Тогда в 8-ой день было (4+1)⋅2=10 рабов. В 7-ой было (10+1)⋅2=22 раба. Вычисляя аналогично, найдем, что в первый день было 1534 раба.
Следующими хотеться рассмотреть две задачи.
Задачи на округление вверх и округление вниз.
Могут ли одни и те же цифры и одни и те же действия с ними привести к разным результатам? Возможно ли это? Давайте разберёмся.
Задача 1: На корабле 700 туристов и 20 членов экипажа. Сколько нужно спасательных лодок? Чтобы в случае аварии спасти всех людей. Одна лодка имеет 50 посадочных мест.
1) 700+20=720 (всего людей на борту)
2) 720:50=14(20человек еще останутся)
Нам нужно спасти всех, значит понадобиться 15 лодок, идет округление вверх.
Задача 2. У Саши 20 рублей в копилке, родители дали еще 700 рублей и попросили его на все деньги купить тетради для школы. Одна тетрадь стоит 50 рублей. Сколько тетрадей купит Саша?
1) 20+700=720 рублей всего
2) 720:50=14 (20 рублей в остатке)
На 20 рублей тетрадь еще одну не купишь, а по пол тетради не продают. Проходит округление вниз. Ответ:14 тетрадей купит Саша.
Как мы увидели одни и те же данные, одни и те же действия дают разные результаты. В одной задачи идет округление вверх, в другой округление вниз. Ответ зависит от текстового смысла задачи.
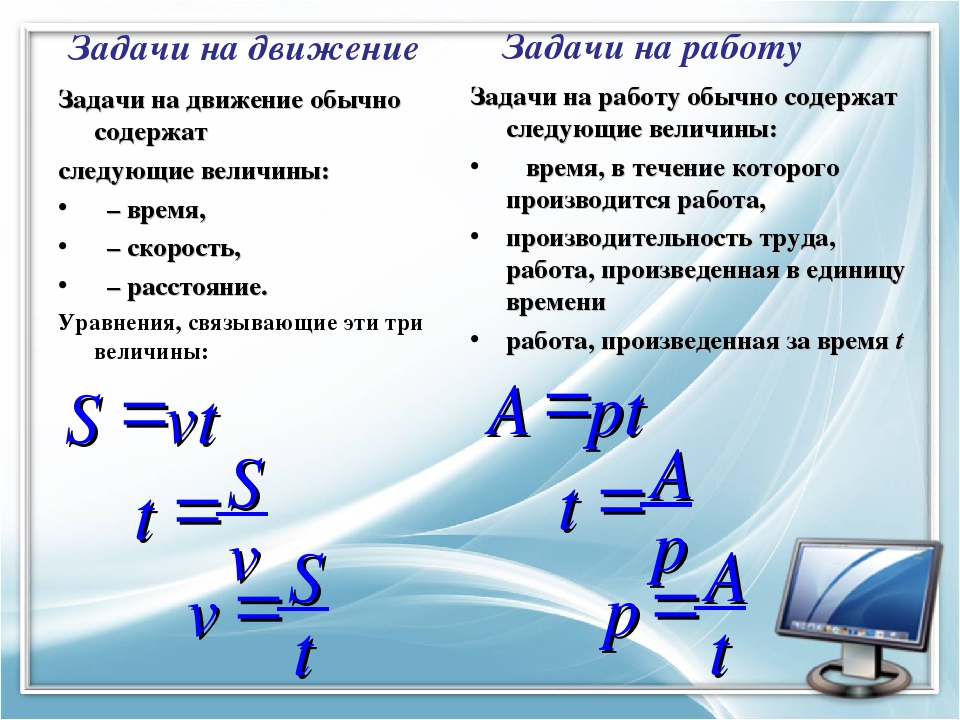
Простые текстовые задачи на движение.
И напоследок рассмотрим задачи на движения, которые относятся к простым текстовым задачам. Их можно решить 3 способами:
1. Способ:
Бегун пробежал 126 м за 18 сек. Найдите среднюю скорость. Ответ дайте в км\ч.
| а) вычислить данные по формуле | 126\18=7м\с |
| б) перевести в искомую единицу измерения | 7м\с=0,007км\с*3600=25,2 км\ч |
2. Способ:
Бегун пробежал 126 м за 18 сек. Найдите среднюю скорость. Ответ дайте в км\ч.
| а) перевести в нужные единицы измерения | 126м-0,126км 18с-1\200ч |
| б) произвести вычисление по формуле | 0,126:1\200=126\5=25,2км\ч |
3. Способ:
Бегун пробежал 126 м за 18 сек. Найдите среднюю скорость. Ответ дайте в км\ч.
| а) вычислить по формуле | 126\18=7м\с |
| Б) умножить (разделить) на 3,6 | 7*3,6=25,2км\ч |
Мы рассмотрели простые и текстовые задачи. Каждая задача требует внимания и сосредоточенности, базовых знаний и способности выстраивать логические структуры. Какой способ вы используете при этом не важно. Важно что бы вы знали все возможности нахождение правильного ответа и оперируя этими знаниями выбрали тот алгоритм (способ), который наиболее подходит для решения поставленной задачи.